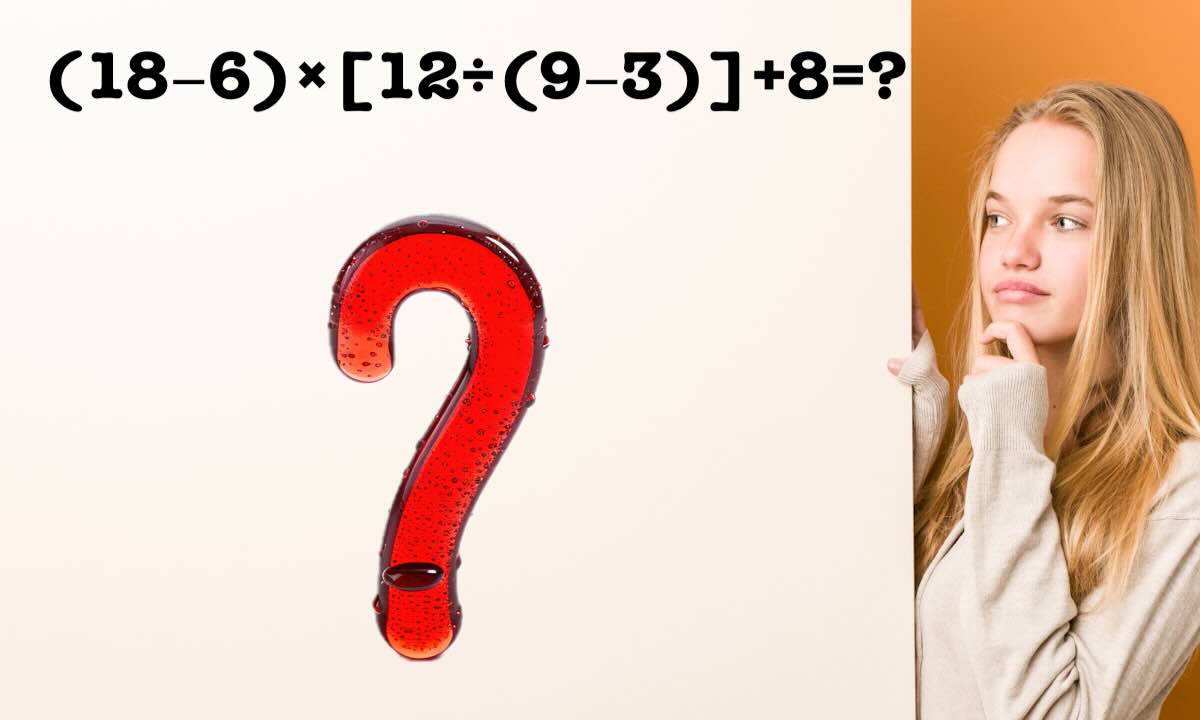test QI : Serez-vous capables de résoudre cette défis mathématique en 15 secondes ?

test QI : Serez-vous capables de résoudre cette mathématique en 15 secondes ?

Les défis mathématiques sont parfaits pour mettre à l’épreuve votre logique et votre rapidité. Aujourd’hui, nous vous proposons une équation qui semble simple à première vue, mais attention, elle peut facilement prêter à confusion. Êtes-vous prêt à relever le défi ?

 (18−6)×[12÷(9−3)]+8.

Qu’est-ce que la règle PEMDAS ?

Avant de vous précipiter, gardez en tête les règles de priorité des opérations (PEMDAS) :

1. Parenthèses : Résolvez ce qui est à l’intérieur des parenthèses et crochets.
2. Multiplication/Division : De gauche à droite.
3. Addition/Soustraction : De gauche à droite.

Avez-vous une réponse à proposer ? Le temps vous a-t-il suffi ? Voyons comment vous devez répondre cette énigme. Sa résolution passe par l’application d’une règle bien précise. Il s’agit de la règle de priorité des opérations.

Deux hypothèses pour résoudre cette défis mathématique :

Hypothèse 1 : Respect strict des priorités des opérations

En suivant les règles PEMDAS à la lettre, vous résolvez d’abord les parenthèses internes, puis les crochets, avant de vous attaquer aux multiplications et additions.

• Parenthèses internes : (9 – 3).
• Résolution des crochets : 12÷(9−3).
• Multiplication principale : (18−6)× [résultat des crochets].
• Addition finale : Ajoutez +8+8.

Cette méthode garantit que l’ordre est respecté et que vous arrivez à une réponse précise.

Hypothèse 2 : Confusion dans les priorités des opérations

Une erreur courante consiste à résoudre les opérations dans l’ordre où elles apparaissent, sans tenir compte des priorités. Par exemple :

• Commencer par (18 – 6).
• Ensuite, diviser 12÷9 sans résoudre correctement le contenu des parenthèses.
• Effectuer ensuite la multiplication et l’addition.

Cette approche peut mener à une réponse différente et incorrecte.

Et vous, quelle méthode utilisez-vous ?

Prenez le temps de réfléchir avant de valider votre réponse. Respecter les règles de priorité des opérations est essentiel pour éviter les erreurs. Une fois votre résultat trouvé, partagez-le avec vos proches pour voir s’ils arrivent au même résultat.

Alors, laquelle de ces hypothèses vous semble correcte ? Faites vos calculs et découvrez la bonne réponse !